Если мы остро отточенным карандашом прикоснемся к листу бумаги, то на нём останется круглый след, который называют точкой. В качестве имени точкам присваивают заглавные латинские буквы: А, В, С и т.д. При объединении множества точек получаются геометрическая фигура. Например, если точки выстроятся вдоль натянутого шнура, то получившаяся фигура даёт представление о прямой линии. С той лишь разницей, что прямая линия является бесконечной, то есть она неограниченно распространяется как в одну,…

Движение вдогонку
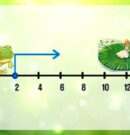
Рассмотрим задачу, в которой объекты, двигаясь в одном направлении, будут сближаться. Жаба, обнаружила пропажу Дюймовочки, и бросилась догонять уносимый быстрым течением лист кувшинки, на котором сидела девочка. Чтобы определить, как ежесекундно изменялось расстояние между ними, то есть их относительная скорость, заполним таблицу зависимости координат Жабы и Дюймовочки от времени, где x1 — координата Дюймовочки, x2 — координата Жабы, d — расстояние между ними. Расстояние между объектами уменьшалось каждую…

Движение с отставанием
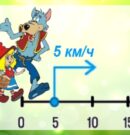
Чтобы понять, от чего зависит относительная скорость объектов, двигающихся в одном направлении, необходимо учесть, что при этом они могут сближаться, но могут и удаляться. Например, рассмотрим такую задачу. Волк объяснил Красной Шапочке, как пройти в бабушкину деревню. Девочка остановилась на полянке с координатой равной пяти и стала собирать для бабушки ягодки и цветочки. Когда она отправилась к бабушке, Волк был уже в точке с координатой 20. И Красная Шапочка, и…

Движение в противоположных направлениях
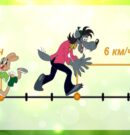
Проиллюстрируем движение объектов в противоположных направлениях на следующей задаче. На вопрос серого Волка: «В какую сторону побежал Заяц?» – Белочка указала противоположное направление. Волк бежал со скоростью 6 км/ч, а Заяц удалялся в противоположном направлении со скоростью 2 км/ч. Если заполнить таблицу зависимости координат Волка и Зайца от времени, где t – время их движения, x1 – координата Волка, x2 – координата Зайца, то можно заметить, как ежечасно изменялось расстояние…

Встречное движение
Рассмотрим такую задачу. Курочка бежит навстречу к своему цыплёнку со скоростью 2 м/с. А цыплёнок приближается к курице со скоростью 1 м/с. Если заполнить таблицу зависимости координат курицы и цыплёнка от времени, где t – время их совместного встречного движения, x1 – соответствующая координата курицы, x2 – координата цыплёнка, то можно заметить, как ежесекундно изменялось расстояние d между ними. Расстояние, на которое приближаются объекты друг к другу за единицу времени,…

Скорость, время, расстояние
Быстрота передвижения Окружающий нас мир находится в постоянном развитии и движении. И людям часто приходится оценивать быстроту перемещения различных объектов наблюдения. Проще это делать, указывая пройденные ими расстояния за равные промежутки времени. Скорость Например, заяц может пробежать за один час 60 км, страус за час – 80 км, гепард за час – 120 км. Говорят, что скорость зайца 60 км в час, страуса – 80 км в час, гепарда –…

Единицы времени
Год, месяц, неделя и сутки – это общеизвестные меры времени. Как они возникли? Посмотрите пояснения на рисунках. Месяцы имеют разную длину. Как определить длину месяца? Почему происходит смена дня и ночи? А как же исчисляется время в течение суток? На циферблате часов расположены числа от 1 до 12, а в сутках 24 часа. Чтобы различить о каком времени суток идёт речь, обычно уточняют: семь часов утра или семь часов вечера….

Задание на лето
Память имеет уникальное свойство вытеснять информацию, которой мы длительное время не пользуемся. Из-за этого каждый год в сентябре и дети, и учителя испытывают огромные трудности, поскольку приходится много времени уделять повторению. При этом текущая программа требует продолжения изучения новых тем. Но всё повторить невозможно, поэтому у многих учеников образуются белые пятна в знаниях или так называемые пробелы. Особенно это заметно в математике, где новые навыки вырабатываются на имеющейся у ребенка…

Разрядные слагаемые
Если начать считать предметы по порядку: один, два, три, четыре, пять и т. д., то есть, добавляя по единичке к каждому предыдущему числу, чтобы перейти к последующему, то дойдя до последнего однозначного числа 9, мы далее получим наименьшее двузначное число – 10. У двузначных чисел мы имеем две позиции для цифр: справа – разряд единиц, слева – разряд десятков. При счёте каждые 10 единичек объединяются в десяток, 10 десятков –…

Деление с остатком
Сказка о том, как Белка к зиме готовилась Собрала как-то белка 16 грибов и решила посушить их на зиму. «Развешу я их поровну на этих трёх ветках, – подумала она. – Красиво будет». Буду действовать так. Сначала на каждую веточку нанижу по одному грибочку, потом по два, потом по три, четыре, пять. У меня останется 1 грибок, но веток 3. Значит, дальше поровну распределить грибы не получится. Развешено по 5…

Площади
Сегодня мы познакомимся с понятием площади, со способами сравнения площадей и их единицами измерения. В математике площадь – это часть плоскости, ограниченная замкнутой ломаной или кривой линией, занимающая какое-то место. В быту под словом площадь подразумевают большое и ровное место. Например, в городе или в селе площадь – это незастроенное пространство, от которого обычно расходятся в разные стороны улицы. Посевная площадь – это пространство, предназначенное для посева, жилая площадь –…

Виды треугольников
Какие же треугольники все разные! Есть ли какие-нибудь свойства, по которым можно было бы их различать? Да, их различают по особенностям углов и длинам сторон. Построение треугольника Как же получить эту фигуру? Поставим три точки на листе бумаги так, чтобы через них нельзя было провести одну прямую линию. Назовём эти точки, например, буквами А, К, М. Обычно точки обозначают заглавными латинскими буквами. Соединим эти точки кусочками прямых линий. Говорят –…
Родительское собрание
Уважаемые родители! Наше родительское собрание посвящается итогам 2 четверти 2020/2021 учебного года. Повестка дня 1.Итоги успеваемости и посещаемости занятий Правила поведения на утреннике Инструктажи по ТБ на зимних каникулах 4.Профилактика ковид-19 5.Горячее питание 6.О выборе программы обучения по ОРКЭС в 4х классах в 2021/2022 уч.году 7.Режим работы школы Ход собрания 1. ПРИМЕРНАЯ ВЕДОМОСТЬ 2 ЧЕТВЕРТЬ Русск.яз. Литер.чт. Род.(рус.) язык Род.(рус) лит.чт. Англ.яз. Математ. Окр.мир Музыка…

Образование и сравнение долей
Разделим апельсин, например, на 8 равных частей. Эти равные части называются долями (апельсиновыми дольками). В нашем случае каждый кусочек – восьмая доля апельсина. Если взять три кусочка – будет три доли. Все, что мы проделали, записывается с помощью чисел, разделенных черточкой. Эту запись назвали обыкновенной дробью: 3/8. Читают дробь так: три восьмых. Запись дробей Для того чтобы записать взятые доли, нужно выполнять действия по следующему правилу: посчитать, на сколько равных долей…