Сегодня мы познакомимся с понятием площади, со способами сравнения площадей и их единицами измерения.
В математике площадь – это часть плоскости, ограниченная замкнутой ломаной или кривой линией, занимающая какое-то место.
В быту под словом площадь подразумевают большое и ровное место.
Например, в городе или в селе площадь – это незастроенное пространство, от которого обычно расходятся в разные стороны улицы.
Посевная площадь – это пространство, предназначенное для посева, жилая площадь – это пространство, предназначенное для жилья, и так далее.
Это понятие используют для того, чтобы можно было оценивать размеры протяженных участков и фигур, сравнивать их между собой.
Какие же существуют в математике способы сравнения размеров плоских фигур?
1 способ. Можно сравнить площади на глаз, когда два предмета расположены рядом. Например, если требуется сравнить площадь пола и ковра, лежащего на нём, или площадь стены и классной доски, висящей на стене, то это легко можно сделать на глаз.
2 способ. Можно сравнить площади способом наложения одной фигуры на другую. Например, мы видим, что если наложить круг на квадрат, то он целиком окажется внутри квадрата. Значит, какая фигура имеет большую площадь? Верно, квадрат.
3 способ. Можно сравнить площади с помощью мерок. Если скопировать первую фигуру и поделить её на несколько одинаковых частей, то эти части можно выбрать в качестве мерки. Выложим эти кусочки на вторую фигуру, и станет ясно, какая из фигур содержит больше таких кусочков. Эта фигура и будет большей.
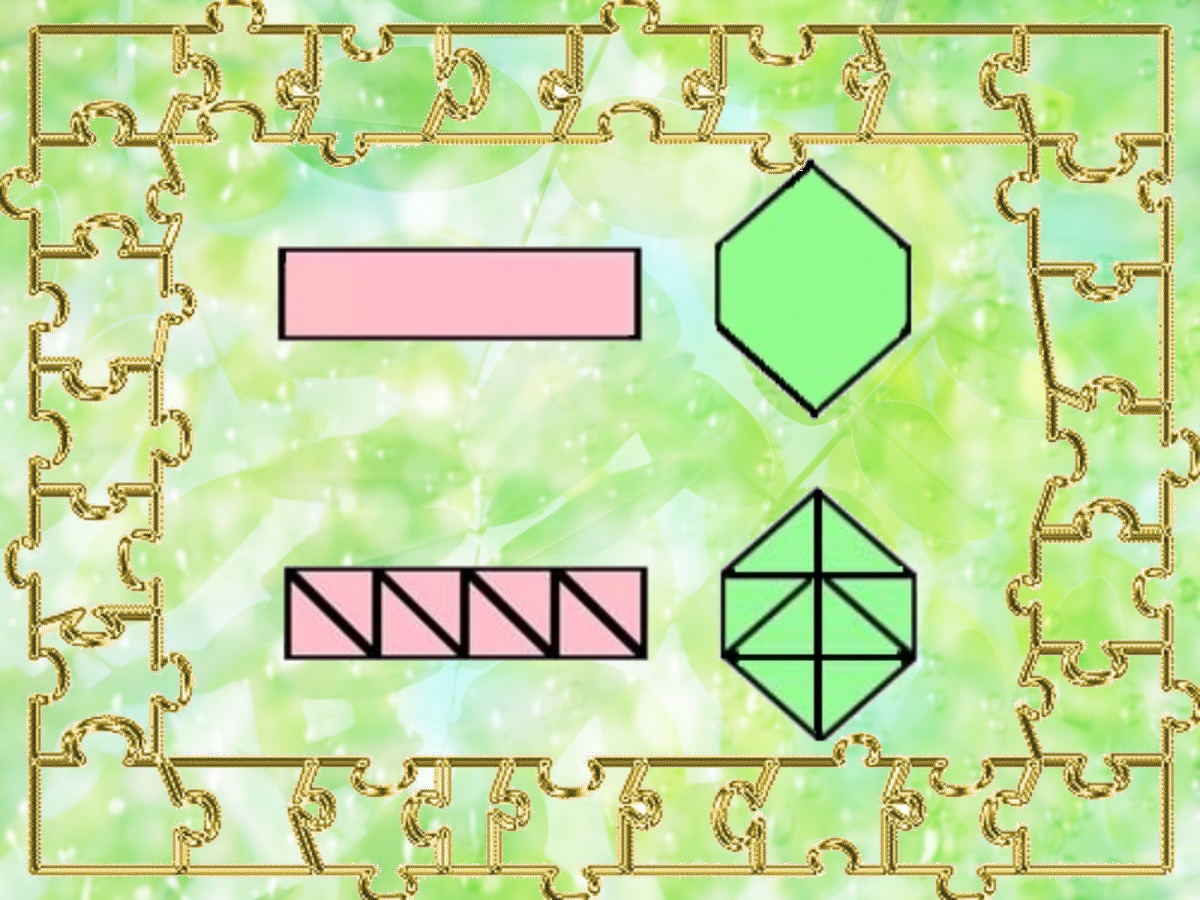
Разделим полоску на равные треугольники, выложим их на поверхность шестиугольника так, чтобы они полностью его покрывали. В данном случае мы видим, что количество треугольников одинаковое. Значит, фигуры имеют равные площади. В математике говорят, что эти фигуры равновеликие.
Самой удобной меркой оказался квадрат. Сравним площади многоугольников, покрывая фигуры равными квадратами. В розовую фигуру уместилось 7 мерок, а в голубую – 8 мерок. Значит, площадь первой фигуры меньше площади второй.
Математики всего мира договорились измерять площади фигур одинаковыми мерками – квадратами, со сторонами единичной длины.
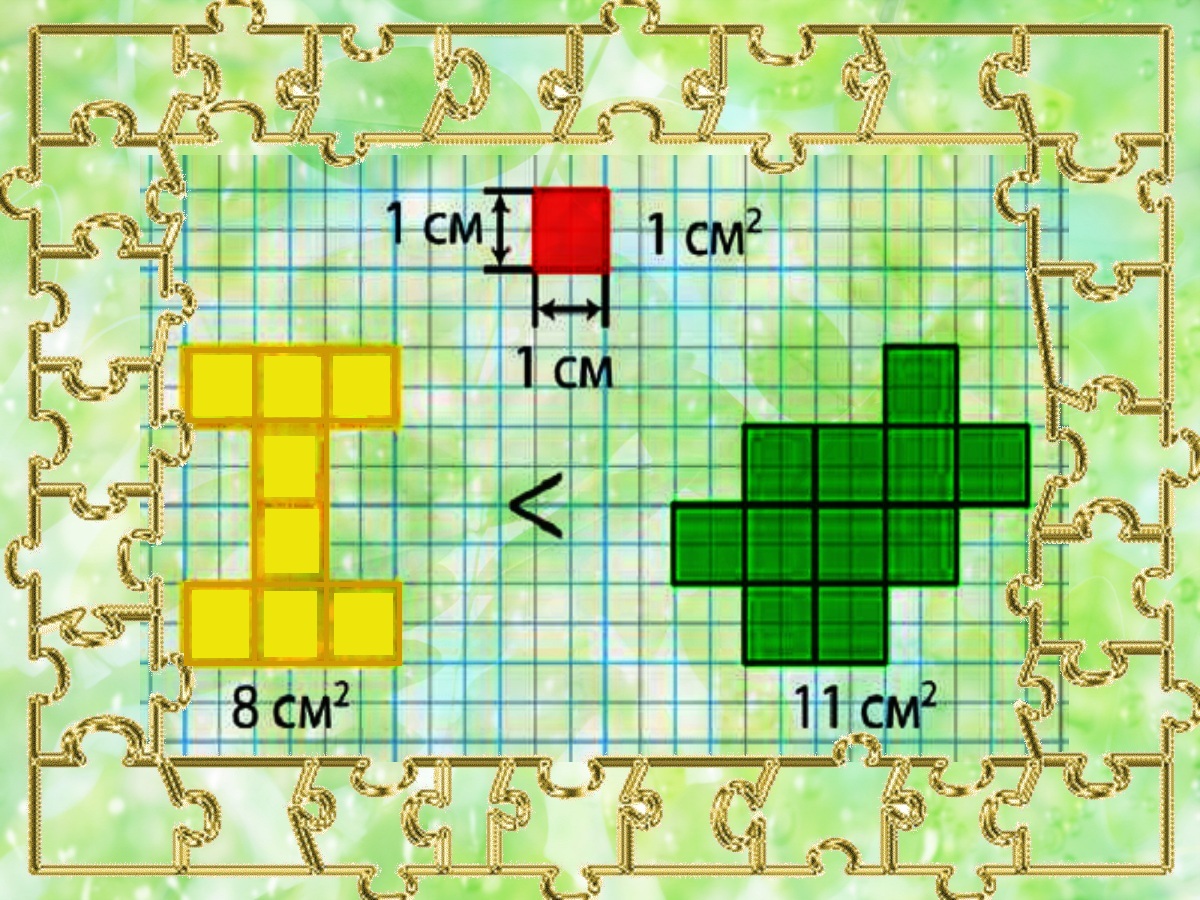
Если взять квадрат, со стороной 1 см, то площадь фигур будет измеряться в квадратных сантиметрах.
В жёлтой фигуре 8 квадратных сантиметров, а в зелёной фигуре – 11 квадратных сантиметров. Значит площадь зелёной фигуры больше, чем площадь жёлтой фигуры.
Очень часто на практике приходится иметь дело с прямоугольниками, поэтому было выведено специальное правило для вычисления площади прямоугольника.
Как найти площадь прямоугольника, длины сторон которого 3 см и 4 см?
Для решения задачи разобьём прямоугольник на 4 полоски по 3 см2 каждая, тогда площадь прямоугольника будет равна 3×4=12 см2.
Для нахождения площади прямоугольника перемножаются числа, выражающие длины сторон прямоугольника. Число 4 обозначает длину прямоугольника, а 3 – ширину прямоугольника. Мы их перемножили и узнали площадь прямоугольника.
Значит, чтобы вычислить площадь прямоугольника, нужно определить его длину и ширину (длины сторон прямоугольника должны быть выражены обязательно в одинаковых единицах измерения), а потом найти произведение этих чисел (площадь будет выражена в соответствующих квадратных единицах площади).
То есть, площадь прямоугольника равна произведению его длины на ширину.
Мы вычислили площадь прямоугольника в квадратных сантиметрах, но, иногда, единицы измерения площади могут быть другими: больше или меньше в десятки раз.
Установим зависимость между квадратным дециметром и квадратным сантиметром. Поскольку квадрат со стороной 1 дм можно разбить на 10 полосок, в каждой из которых по 10 см2, то всего в квадратном дециметре десять десятков, или сто квадратных сантиметров.
Запомните: 1 дм2 = 100 см2.
Установим соотношение между квадратным дециметром и квадратным метром. Поскольку квадрат со стороной 1 м можно разбить на 10 полосок, в каждой из которых по 10 дм2, то всего в квадратном метре десять десятков, или сто квадратных дециметров.
Запомните: 1 м2 = 100 дм2.